The Dijkstra QuickSort...
About two years ago, a colleague was developing a kernel driver; all of his tests were running great, until a kernel panic happened on a reboot. After investigating it for a while, it turned out that the driver was using the QuickSort algorithm, and it ran out of stack space. While it is sometimes easier to find another algorithm, sometimes it is just as easy to unroll your recursion, and the QuickSort algorithm is an easy one to unroll.
First, let's start by considering a a standard QuickSort algorithm, such as from Data Structures and Algorithms in C by Mark Allan Weiss (which is also on Algorithms and Data Structures Version 2 CD-ROM). I have implemented a class in Java that implements a basic case, called RecursiveQuickSort (for convenience, it derives from QuickSort). There is not a lot of fancy things going on. The algorithm selects a pivot point, swapping some elements whilst it is there, and then recurses.
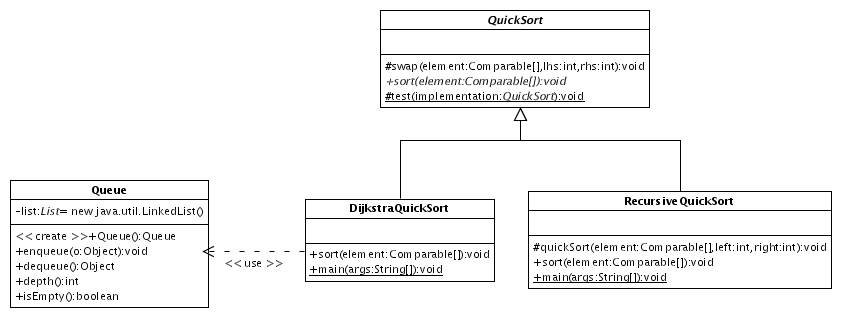
One of the easiest ways to remove the recursion is to use a technique similar to that employed by Dijkstra's unweighted shortest-path algorithm. By creating a queue of the quickSort() parameters, the algorithm can simply be unrolled, as I have done in DijkstraQuickSort. As Java does not have a Queue class in 1.4 (there is a generic one in 1.5), I had to implement a very simple Queue class using a List.
The core algorithm is essentially just wrapped in the queue manipulation algorithm that comes from the Dijkstra algorithm. Of course, while this is incredibly simple, this does beg the question of whether allocating a Queue on the heap is more efficient some function calls on the stack, but this really depends on your environment. If you have limited heap also, you may want to consider another algorithm. But in the IRIX kernel, we had ample memory available to us, so this solution worked quite nicely.